量子電腦程式原理

首先,讓我們首先了解什麼是量子電腦? 以及它們與電子電腦的不同之處?

量子電腦是使用量子力學進行計算的機器。

那麼，這與其他電腦有何不同？嗯，最早期基本形式的電腦就是單純執行計算的機器。在1837年設計了查爾斯·巴貝奇（Charles Babbage）這樣的機械式機器來執行通用計算。如今，我們的電腦基於數字電子設備，並使用位元和邏輯閘進行操作。相反，量子電腦使用量子力學進行計算。量子電腦不是使用電子位元和邏輯閘，而是使用量子位元(qubit)和量子閘。

量子程式

量子程式不僅是使現有某些程序運行更快的一種方式,量子程式與現代程式在根本上是不同的。

量子位元

量子位元是具有單位長度的兩個複數的向量。

量子位元與電子位元完全不同。一位元是0或1。它要嘛是0，要嘛是1。相反，一個量子位本質上是機率性的，兩個相同的量子位一旦測量！可能具有不同的值。量子計算本質上是機率性的。

第二個關鍵區別。使用電子位元，可以根據需要多次讀取位，而不會影響位的狀態。但是對於量子位元，一旦被測量，它就會去相干（失去其量子特性）並坍塌為兩個可測量狀態之一（因此，“量子位元”中的“位元”）。因此，我們不能“測量”一個量子位元。一旦測量，量子性質將被破壞，無法恢復。我們使用兩個數來量化測量量子位元的機率性質：｜ 𝛼 ｜²，量子位元的機率為0，｜ 𝛽 ｜²，量子位元的機率為1。

儘管｜ 𝛼 ｜²和｜ 𝛽 ｜²反映了量子位將被測量的概率，但我們將量子位元的內部狀態視為兩個“機率幅度”'𝛼和𝛽。這些是複數，定義了0到1之間的疊加（疊加是線性組合）並且無法測量。

換句話說，我們將量子位元視為具有單位長度的兩個複數的向量（向量的長度等於1）。可以簡明地將其表示為數學形式，如下圖所示（包含𝛼和𝛽的向量是qubit； 𝛼和𝛽上方的條表示共軛複數）：

量子位元符號

我們通常使用Dirac表示法（也稱為Bra-ket表示法）表示量子位元。這種表示法只是編寫向量的一種簡便方法。bra代表行向量並表示⟨ ∣; ket表示列向量，並用表示∣ ⟩。例如，我們可以按如下所示用Bra-ket表示法來表示qubit的'0'和'1'狀態：

量子位元可以處於純狀態或混合狀態。如果一個量子位元的狀態可以使用的線性組合來全面地描述∣0⟩和∣1⟩，則我們說其在純狀態。我們通常使用以下表示法表示純狀態量子位：

這是一些純態量子位元的例子，以及表示它們的常用簡寫。

其他量子位元需要純狀態的混合才能充分描述它們，因此我們稱它們為混合狀態量子位元。換句話說，混合態量子位元是通過純態上的概率分佈來描述的。

多個量子位元

多個量子位的組合狀態是所有量子位的張量積。

什麼是張量積？如下範例（⊗是張量積運算的符號）。

通常，我們可以通過以下兩個步驟對任何兩個矩陣進行張量積：

1. 標量將第一矩陣中的每個元素乘以整個第二矩陣
2. 根據元素的原始位置合併結果矩陣

這是如何處理二維矩陣的第二個範例：

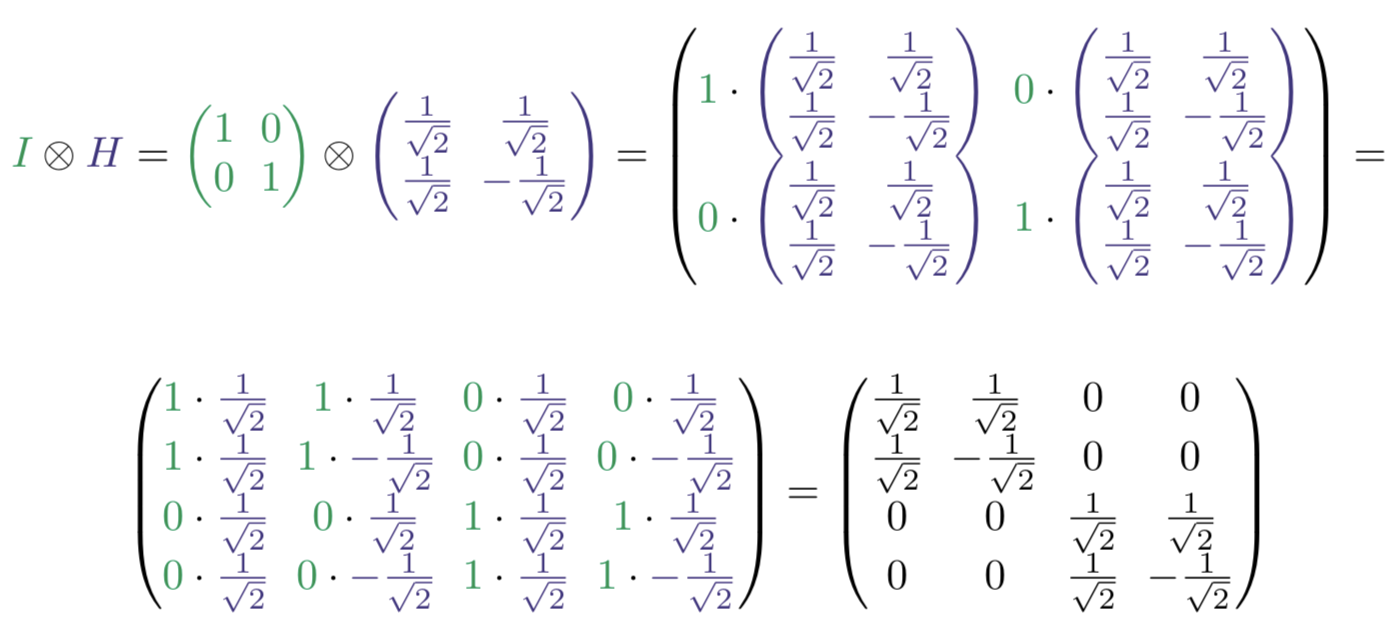
例如，我們也可以用Bra-ket表示法表示多個量子位∣0⟩⊗∣1⟩。作為簡寫，我們可以省略⊗並簡單地寫∣0⟩∣1⟩。作為更簡短的縮寫，我們可以只寫一個ket ∣01⟩。

量子閘

量子閘是一個矩陣。

量子閘將應用於量子位元。量子位元實際上只是向量，這意味著量子閘必須以某種方式對向量起作用。矩陣實際上只是向量的線性變換！

結合這兩種思想，我們將量子閘視為單一矩陣。矩陣是複數的任何方陣，因此共軛轉置等於它的逆。可以通過獲取矩陣中每個元素的共軛（a + bi→ a — bi），然後取矩陣的轉置（元素ij→元素ji）來找到矩陣的共軛轉置。我們通常用匕首†表示共軛轉置。

單位矩陣的一個關鍵發現是它們保留了範數（向量的長度）。所有機率的總和必須始終等於1。

量子閘是單位矩陣，從定義上來說它們是正方形的，所以量子閘必須具有相等數量的輸入和輸出量子位元,這與電子邏輯閘完全不同。例如，AND閘有兩個輸入一個輸出。

H和CNOT量子閘

阿達馬閘（Hadamard gate）H。

我們可以通過檢查共軛轉置等於其逆數來檢查H是否為一，換句話說，將H與其共軛轉置相乘等於單位矩陣：

另一個重要的量子閘是受控反閘，也稱為CNOT。CNOT作用於兩個量子位元，即控制量子位元和目標量子位元。我們可以將CNOT視為“ if語句” -如果控制量子位元等於1，則CNOT將NOT（反向閘）應用於目標量子位（因此，其名稱為Controled NOT）。

這是代表CNOT的矩陣。該矩陣將控制量子位元視為ket內部最右邊的值，將目標量子位元視為最左側值。

讓我們看看它對的影響∣00⟩。

在此示例中，我們看到CNOT不會修改的值∣00⟩。這是預期的行為，因為CNOT僅在控件為1時才反轉目標。

讓我們看看它對的影響∣01⟩。

在這裡，我們可以看到控件等於1，因此CNOT反轉了目標。因此，結果是∣11⟩。

嘗試找出另外兩種情況，∣10⟩並∣11⟩。CNOT具有以下行為：

• ∣00⟩ -> ∣00⟩
• ∣01⟩ -> ∣11⟩
• ∣10⟩ -> ∣10⟩
• ∣11⟩ -> ∣01⟩

量子電路圖

下面是一個量子電路圖。

量子電路圖是我們對量子“程序”的思考。我們將量子位元定義為行，然後從左到右依次應用量子閘。

首先，我們有兩個量子位元。每行對應一個量子位元。最上面一行對應於名為x0的量子位元，最下面一行對應於名為x1的量子位元。我們將x0視為第0個量子位元，因為我們從0開始計數（與其餘程式相同）。我們寫x0 : ∣0⟩並x1 : ∣0⟩ 表示這一點，x0然後x1從狀態開始∣0⟩。

H是哈達瑪柵極和被施加到量子位元X0。●-⊕是CNOT閘，●是控制量子位元，並且⊕是靶標量子位元。-只是幫助我們看到這兩個量子位元受到影響。換句話說，我們正在應用CNOT，其中控件為qubit x0，目標為x1。請注意，我們應用這些閘的順序很重要。在此圖中，我們首先應用H，然後應用CNOT。

翻譯量子電路圖

量子電路圖只是我們程序的一種表示。它可以幫助我們考慮量子計算，但其他表示形式也可能有用。我們可以將圖表轉換為符號字符串，這在準備將其編寫為電腦代碼時會有所幫助。以字符串形式包含它也可以輕鬆地轉換為基礎數學。這個數學運算將告訴我們程序的預期輸出。

讓我們從將圖表轉換為符號字符串開始。我們將使用Bra-ket表示法，而不是將我們的量子位元寫為行。∣00⟩就像寫二進制數²一樣，第0個量子位元將是中最右邊的量子位元。這意味著qubit x1是中最左邊的qubit ∣00⟩。（請注意，量子物理學家傾向於顛倒這種順序³。請始終檢查量子位元的順序，因為它是非常常見的錯誤來源。）

由於我們要應用H到qubit x0而不是應用任何東西到qubit x1（等同於應用Identity Gate，I），因此我們將其寫為(I⊗H)。最後，我們翻譯CNOT，指定哪個qubit是控件，哪個是目標。結果是CNOT[control=0, target=1] (I⊗H) ∣00⟩ （請注意，該字符串是從右到左讀取的）。當編寫將在量子電腦上運行的代碼時，這將非常有用。

寫出基礎數學

擁有量子電路圖的字符串表示形式，可以輕鬆地將我們的程序轉換為基礎數學。有三件，CNOT[control=0, target=1]，(I⊗H)，和∣00⟩。每個片段都可以轉換為矩陣，如下圖的第一行所示：

我們甚至可以將矩陣相乘以找到結果狀態向量，如上所示。該狀態向量是量子計算完成後兩個量子位的預期狀態。另外，我們可以將其視為程序的輸出。它告訴我們每種可測量狀態的概率幅度。

另外，還記得我們的混合狀態量子位嗎？注意，我們不再能夠以純狀態實際寫入qubit x0和qubit x1了，因為沒有任何方法可以用張量積分解向量。因此我們的量子位處於混合狀態！

測量狀態向量

如果我們現在測量量子比特怎麼辦？我們會收到什麼？我們可以通過將狀態向量分解為每個可測量狀態來找出。我們將以標準的基礎（也稱為∣0⟩和）來衡量我們的量子位∣1⟩（還有其他可以衡量的基礎，但現在不必擔心）。因此，我們這兩個量子比特系統的可衡量的狀態是∣00⟩，∣01⟩，∣10⟩，和∣11⟩。

我們可以像使用｜ 𝛼 ｜²來確定∣0⟩單個量子位的概率一樣，來確定測量值的概率。由於∣01⟩且∣10⟩振幅為0，所以我們知道我們永遠也不會測量該狀態。而且，我們將同時測量∣00⟩和∣11⟩以概率（1 / SQRT（2））2 = 1/2。

現在，假設我們將這兩個量子比特分開很長的距離，然後我們測量了其中一個。我們測量它的那一刻，我們也將知道另一個量子比特的價值！這是因為我們知道量子位只能是∣00⟩或∣11⟩。

這就是愛因斯坦所說的“遠距離的鬼妹效應”，也稱為量子糾纏。我們認為信息是相關的，而不是旅行的。如果它正在旅行，那麼它的傳播速度可能會比光快，這會破壞物理定律。

在Quantum電腦上運行

現在，我們了解了量子位元，量子閘和量子電路圖在幕後發生的事情，讓我們看看如何在真實的量子電腦上運行。我將使用Rigetti的量子電腦，因為他們目前向beta用戶免費贈送信用。或者，我們也可以使用IBM的量子電腦。

這是Rigetti量子程式過程的基本概述：

1. 編寫一個Python程序，指定您的量子電路和任何其他必需的代碼
2. 使用量子模擬器測試該Python程序
3. 在Rigetti的量子電腦上保留時間
4. 將您的程序發送到Rigetti的服務器
5. 在Rigetti的服務器上執行程序（它們將為你將量子程序發送到他們的量子電腦）

這是上面的量子電路圖的Python版本。

from pyquil.quil import Program
from pyquil.api import *
from pyquil.gates import *

# 將H應用於qubit 0，然後將CNOT應用於qubit 0和1
p = Program(H(0), CNOT(0, 1))
# 獲取有關2個量子位元量子虛擬電腦的信息
qc = get_qc('2q-qvm')
#模擬程式
results = qc.run_and_measure(p, trials=10)
print(list(zip(results[0], results[1])))

# 將H應用於qubit 1，然後將CNOT應用於qubit 1和2
p = Program(H(1), CNOT(1, 2))
# 獲取有關名為Aspen-4-2Q-A的真實2量子位元量子電腦的信息
qc = get_qc('Aspen-4-2Q-A')
# 將程序發送到量子電腦並運行
results = qc.run_and_measure(p, trials=10)
print(list(zip(results[1], results[2])))

結果將類似於以下內容：

[（0，0），（1，1），（1，1），（0，0），（0，0），（0，0），（1，1），（0，0），（ 0，0），（1，1）] 

[（0，0），（0，1），（1，1），（1，1），（1，1），（0，0），（0 ，0），（1，1），（1，0），（0，0）]

第一行對應於模擬器，結果似乎合理-我們得到[0，0]大約是一半的時間，而[1，1]是剩餘的時間。但是，對於真實的量子電腦，除了期望的[0，0]和[1，1]，我們還收到[0，1]和[1，0]。根據數學計算，我們應該永遠只收到[0，0]和[1，1]，所以怎麼回事？

問題在於，今天的真實量子電腦仍然很容易出錯。⁴例如，當嘗試將qubits初始化為0時，我們可能會看到2–3％的錯誤率。而且我們可能還會有1-2每個單量子位門操作的錯誤率為％，而兩個量子位門操作的錯誤率約為3-4％。測量量子比特時，我們甚至有錯誤率！實際上，這些錯誤會累積並導致錯誤的值。

我們了解到量子電腦實際上確實存在並且可以正常工作，儘管錯誤率很高。儘管這些機器的物理實現在不同公司之間存在很大差異，但對它們進行程式的許多概念仍然相同。

我們認為量子位元是具有單位長度的兩個複數的向量，並且我們將量子閘視為單位矩陣。我們記得量子計算是概率性的，因為一旦測量，兩個相同的量子位可能具有不同的值。而且由於量子閘是單一的，我們知道量子計算本質上是可逆的。在較高的層次上，我們可以將量子程式視為對複數應用的線性代數。

我們使用量子電路圖來表示我們的量子程序，然後將其轉換為Python以在真實的量子電腦上運行。

---

參考文獻

[1] L. Susskind，第1講量子糾纏，第1部分（2008）

[2] Qiskit（2019）中的基礎向量排序，Qiskit

[3] R. Smith，有人喊“ 01000”！誰激動？（2017），arxiv

[4] Qubit Quality（2019），量子計算報告

[5]Quentin Truong ,DATA SCIENCE Introduction to Quantum Programming